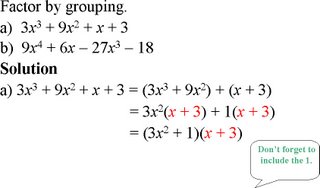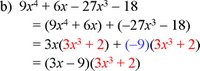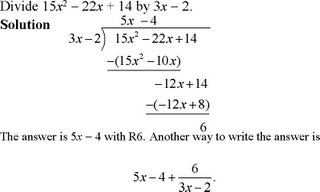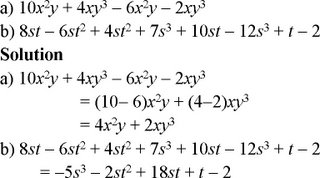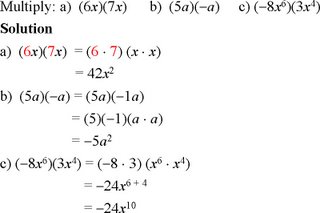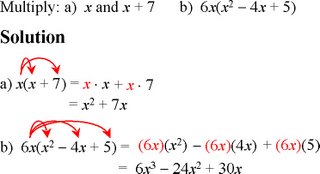Introductory Algebra: October 2006

Polynomials: Factoring 5.1

5.1 INTRODUCTION TO FACTORING
a. Find the greatest common factor, the GCF, of monomials.
b. Factor polynomials when the terms have a common factor, factoring out the greatest common factor.
c. Factor certain expressions with four terms using factoring by grouping.

Objective a
Find the greatest common factor, the GCF, of monomials.

The numbers 20 and 30 have several factors in common, among them 2 and 5. The greatest of these common factors is called the greatest common factor, GCF. One way to find the GCF is by making a list of the factors of each number.
The factors of 20: 1, 2, 4, 5, 10, and 20
The factors of 30: 1, 2, 3, 5, 6, 10, 15, and 30
Common numbers: 1, 2, 5, and 10.
The GCF is 10.
Another way to find the GCF is to find the prime factorization of each number. Then draw lines between common factors.

Example A

Example B

Example C

To Find the GCF of Two or more Monomials

Objective b
Factor polynomials when the terms have a common factor, factoring out the greatest common factor.

Factoring When Terms Have a Common Factor

Example D

Example E

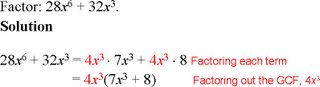
Example F

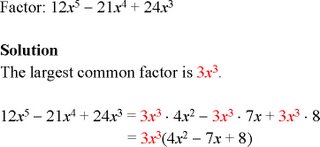
Example G

Example H

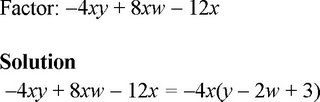
Objective c
Factor certain expressions with four terms using factoring by grouping.

Factoring by Grouping

If a polynomial can be split into groups of terms and the groups share a common factor, then the original polynomial can be factored. This method, known as factoring by grouping, can be tried on any polynomial with four or more terms.

Example J

Polynomials: Operations 4.8

4.8 DIVISION OF POLYNOMIALS
a. Divide a polynomial by a monomial.
b. Divide a polynomial by a divisor that is a binomial.

Objective a
Divide a polynomial by a monomial.

Example A

Example B

Example C

To divide a polynomial by a monomial, divide each term by the monomial.

Objective b
Divide a polynomial by a divisor that is a binomial.

Dividing by a Binomial
For divisors with more than one term, we use long division, much as we do in arithmetic. Polynomial are written in descending order and any missing terms in the dividend are written in, using 0 for the coefficients.

Example D

Example E

Example F

Polynomials: Operations 4.7

4.7 OPERATIONS WITH POLYNOMIALS IN SEVERAL VARIABLES
a. Evaluate a polynomial in several variables for given values of the variables.
b. Identify the coefficients and the degrees of the terms of a polynomial and the degree of a polynomial.
c. Collect terms of a polynomial.
d. Add polynomials.
e. Subtract polynomials.
f. Multiply polynomials.

Objective a
Evaluate a polynomial in several variables for given values of the variables.

Example A

Example B

Objective b
Identify the coefficients and the degrees of the terms of a polynomial and the degree of a polynomial.

Objective c
Collect terms of a polynomial.

Like Terms

Example C Combine like terms.

Objective d
Add polynomials.

Example D

Objective e
Subtract polynomials.

Example E

Objective f
Multiply polynomials.

Example F

Polynomials: Operations 4.6

4.6 SPECIAL PRODUCTS
a. Multiply two binomials mentally using the FOIL method.
b. Multiply the sum and the difference of two terms mentally.
c. Square a binomial mentally.
d. Find special products when polynomial products are mixed together.

Objective a
Multiply two binomials mentally using the FOIL method.

Example A

Example B

Objective b
Multiply the sum and the difference of two terms mentally.

Example C

Objective c
Square a binomial mentally.

Example D

Objective d
Find special products when polynomial products are mixed together.

Example E Multiply.

Polynomials: Operations 4.5

4.5 MULTIPLICATION OF POLYNOMIALS
a. Multiply monomials.
b. Multiply a monomial and any polynomial.
c. Multiply two binomials.
d. Multiply any two polynomials.

Objective a
Multiply monomials.