Prealgebra Review Sections R1 and R2
Prealgebra Review
R.1 Factoring and LCMs
R.2 Fraction Notation
R.3 Decimal Notation
R.4 Percent Notation
R.5 Exponential Notation and Order of Operations
R.6 Geometry
R.1 FACTORING AND LCMS
a. Find all the factors of numbers and find prime factorizations of numbers.
b. Find the LCM of two or more numbers using prime factorizations.
Objective a
Find all the factors of numbers and find prime factorizations of numbers.
Example A
Find all the factors of 72.
Solution
Check sequentially the numbers 1, 2, 3, and so on, to see if we can form any factorizations.
1 × 72
2 × 36
3 × 24
4 × 18
6 × 12
8 × 9
Prime Number
A natural number that has exactly two different factors, itself and 1, is called a prime number.
Example B
Determine whether the numbers listed below are prime, composite, or neither.
8
Has factors of 1, 2, 4 and 8, composite
13
Has only two factors 1 and itself, prime
24
Has factors 1, 2, 3, 4, 6, 8, 12, 24, composite
33
Has factors 1, 3, 11, 33, composite
85
Has 5 as a factor, composite
97
Has only two factors 1 and itself, prime
Example C
Find the prime factorization of 50.
Solution
a) Since 50 is even, it must have 2 as a factor.
50 / 2 = 25
b) Since 25 ends in 5, we know 5 is a factor.
25 / 5 = 5
Because 5 is prime, we can factor no further.
The prime factorization can be written as 2 × 5 × 5 or 2 × 52
Example D
Find the prime factorization of 48 using a factor tree.
Solution
48 = 6 × 8 = 2 × 3 × 2 × 4 = 2 × 3 × 2 × 2 × 2 = 48
Example E
Find the prime factorization of 220.
Solution
220 = 22 × 10 = 2 × 11 × 2 × 5 = 2 × 2 × 5 × 11 = 220
Example F
Find the prime factorization of 1424.
Solution
We use a string of successive divisions.
1424 / 2 = 712
712 / 2 = 356
356 / 2 = 178
178 / 2 = 89
1424 = 2 × 2 × 2 × 2 × 89
Objective b
Find the LCM of two or more numbers using prime factorizations.
Example G
Find the LCM of 40 and 60.
Solution
a) First list multiples of 40 and 60.
40, 80, 120, 160, 200, 240, 280, …
60, 120, 180, 240, …
c) Circle the multiples that appear in both lists.
d) The common multiples of 40 and 60 are 120 and 240. The LCM is 120.
To find the LCM of several numbers using prime factorizations:
a) Write the prime factorization of each number.
b) Form the LCM by writing the product of the different factors from step (a), using each factor the greatest number of times that it occurs in any one factorization.
Example H
Find the LCM of 35 and 90.
Solution
a. Find the prime factorization of each number.
35 = 5 × 7
90 = 2 × 3 × 3 × 5
b. The different prime factors are 2, 3, 5, and 7. We write 2 as a factor one time.
The 3 occurs at most two times.
The 5 occurs at most one time.
The 7 at most one time.
2 × 3 × 3 × 5 × 7 The LCM is 630.
Example I
Find the LCM of 36 and 48.
Solution
a. Write the prime factorization of each number:
36 = 2 × 2 × 3 × 3
48 = 2 × 2 × 2 × 2 × 3
b. Look for the greatest number of times each factor occurs.
2 occurs as a factor 4 times
3 occurs as a factor 2 times
LCM = 2 × 2 × 2 × 2 × 3 × 3 = 144
Example J
Find the LCM of 15, 30 and 25.
Solution
a. Write the prime factorization of each number.
15 = 3 × 5 30 = 2 × 3 × 5 25 = 5 × 5
b. We write 2 as a factor one time
3 occurs as a factor one time
5 occurs as a factor two times
The LCM = 2 × 3 × 5 × 5 = 150
If one number is a factor of another, then the LCM is the larger of the two numbers.
If two or more numbers have no common prime factor, then the LCM is the product of the numbers.
R.2 FRACTION NOTATION
a. Find equivalent fraction expressions by multiplying by 1.
b. Simplify fraction notation.
c. Add, subtract, multiply and divide using fraction notation.
Objective a
Find equivalent fraction expressions by multiplying by 1.
The following are some examples of fractions: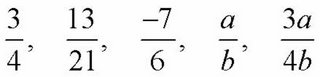
This way of writing number names is called fraction notation. The top number is called the numerator and the bottom number is called the denominator.
Arithmetic Numbers
The arithmetic numbers are the whole numbers and the fractions, such as 8, ¾, and 6/5. All these numbers can be named with fraction notation a/b, where a and b are whole numbers and b does not equal 0.
The Identity Property of 0 (Additive Identity)
For any number a,
a + 0 = a.
(Adding 0 to any number gives that same number—for example 12 + 0 = 12.)
The Identity Property of 1 (Multiplicative Identity)
For any number a,
a × 1 = a.
(Multiplying any number by 1 gives that same number—for example 2 × 1 = 2.)
Equivalent Expressions for 1
For any number a, a does not equal 0,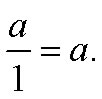
Example A
Find a number equivalent to 3/4 with a denominatorof 36.
Solution
Since 36 / 4 = 9, we multiply by 1, using 9/9:
Objective b
Simplify fraction notation.
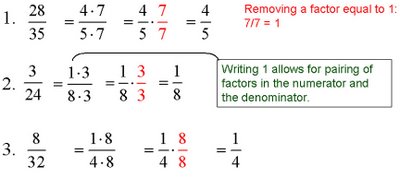
Example B
Simplify.
Solution.
Canceling
Canceling is a shortcut that you may have used for removing a factor that equals 1 when working with fraction notation.
Canceling may be done only when removing common factors in numerators and denominators.
Canceling must be done with care and understanding.
Caution
The difficulty with canceling is that it is often applied incorrectly in situations like the following: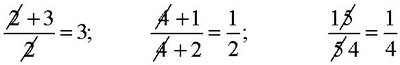
The correct answers are: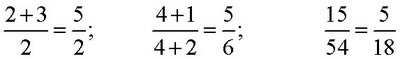
In each of the incorrect cancellations, the numbers canceled did not form a factor equal to 1. Factors are parts of products, but in 2 + 3, the numbers 2 and 3 are terms. You cannot cancel terms.
Objective c
Add, subtract, multiply and divide using fraction notation.
Multiplying FractionsTo multiply fractions, multiply the numerators and multiply the denominators:
Example C
Multiply and simplify.
Solution.
Removing a factor equal to 1.
Adding Fractions with Like Denominators
To add fractions when the denominators are the same, add the numerators and keep the same denominator:
Example D
Add and simplify.
Solution.
Adding Fractions with Different Denominators
To add fractions when denominators are different:
a) Find the least common multiple of the denominators. That number is the least common denominator, LCD.
b) Multiply by 1, using an appropriate notation, n/n, to express each number in terms of the LCD.
c) Add the numerators, keeping the same denominator.
d) Simplify, if possible.
Example E
Add
Solution
a) The LCD is 10. 5 is a factor of 10 so the LCM of 5 and 10 is 10.
b) We need to find a fraction equivalent to 1/5 with a denominator of 10:
c & d) We add:
Example F
Add:
Solution
The LCD is 36. 12 = 2 × 2 × 3 18 = 2 × 3 × 3 LCM = 2 × 2 × 3 × 3, or 36
Example G
Subtract:
Solution
The LCM of 7 and 5 is 35, so the LCD is 35.
Find equivalent numbers with denominators of 35.
We subtract:
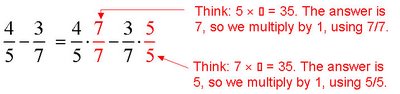
Example H
Subtract
Solution
Determine the LCM of 12 and 16.
Reciprocals
Two numbers whose product is 1 are called reciprocals, or multiplicative inverses, of each other.
Example I
Find the reciprocal.
Dividing Fractions
To divide fractions, multiply by the reciprocal of the divisor:
Solution
Example K
Divide and simplify.
Solution
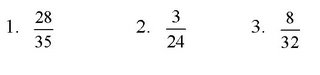
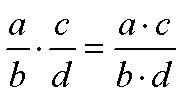
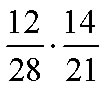
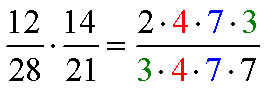

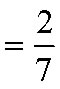
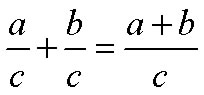
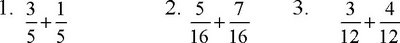
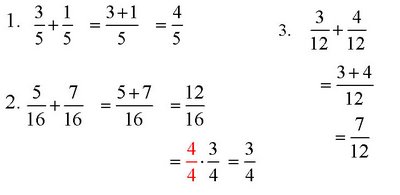
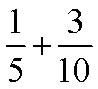
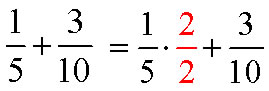
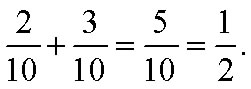
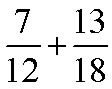
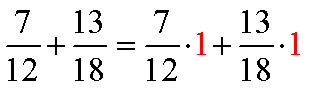


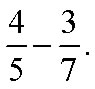
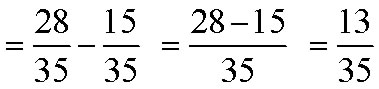
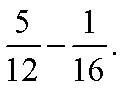

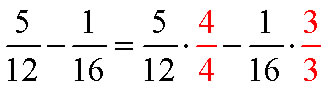
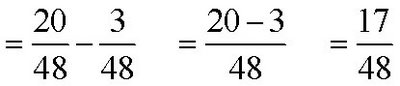


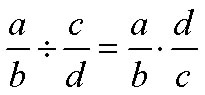
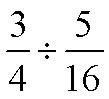



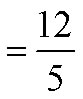



0 Comments:
Post a Comment
Subscribe to Post Comments [Atom]
<< Home