Introduction to Real Numbers and Algebraic Expressions 1.2

1.2 The Real Numbers

a. State the integer that corresponds to a real-world situation.
b. Graph rational numbers on a number line.
c. Convert from fraction notation to decimal notation for a rational number.
d. Determine which of two real numbers is greater and indicate which, using <>; given an inequality like a > b, write another inequality with the same meaning. Determine whether an inequality like -3 £ 5 is true or false.
e. Find the absolute value of a number.

Objective a
State the integer that corresponds to a real-world situation.

Natural Numbers
The set of natural numbers = {1, 2, 3, …}. These are the numbers used for counting.

Whole Numbers
The set of whole numbers = {0, 1, 2, 3, …}. This is the set of natural numbers with 0 included.

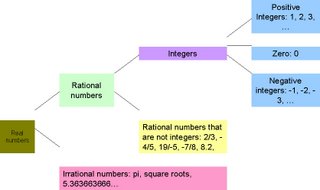
Integers
The set of integers = {…, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, …}.

Integers



Example A

Tell which integer corresponds to each situation.
1. Death Valley is 282 feet below sea level.
2. Margaret owes $312 on her credit card. She has $520 in her checking account.

Solution
1. 282 below sea level corresponds to -282.
2. The integers -312 and 520 correspond to the situation.

Objective c
Graph rational numbers on a number line.



Rational Numbers



To graph a number means to find and mark its point on the number line.



Example C



Objective c
Convert from fraction notation to decimal notation for a rational number.

Each rational number can be named using fraction notation or decimal notation.

Example D



Example E



Objective d
Determine which of two real numbers is greater and indicate which, using <>; given an inequality like a > b, write another inequality with the same meaning. Determine whether an inequality like -3 <= 5 is true or false.

Decimal notation for rational numbers either terminates or repeats. Decimal notation for irrational numbers neither terminates nor repeats.

The Real-Number Systems
The set of real numbers = The set of all numbers corresponding to points on the number line.




Numbers are written in order on the number line, increasing as we move to the right. For any two numbers on the line, the one to the left is less than the one to the right.

The symbol <> means “is greater than,”
-6 > -9 is read “-6 is greater than -9.”

Example F



Example G



Order; >, <> a.

Example H
Write another inequality with the same meaning.
a. -4 > -10
b. c < -7 Solution a. The inequality -10 < -4 has the same meaning. b. The inequality -7 > c has the same meaning.



Objective e
Find the absolute value of a number



Absolute Value
The absolute value of a number is its distance from zero on a number line. We use the symbol x to represent the absolute value of a number x.

Finding Absolute Value
a) If a number is negative, its absolute value is positive.
b) If a number is positive or zero, its absolute value is the same as the number.

Example I

Find the absolute value of each number.
a. -5
b. 36
c. 0
d. -52

Solution
a. -5 The distance of -5 from 0 is 5, so - 5 = 5.
b. 36 The distance of 36 from 0 is 36, so 36 = 36.
c. 0 The distance of 0 from 0 is 0, so 0 = 0.
d. -52 The distance of -52 from 0 is 52, so -52 = 52.