Introduction to Real Numbers and Algebraic Expressions 1.3

ADDITION of REAL NUMBERS 1.3
a. Adding real numbers without using a number line.
b. Find the opposite, or additive inverse, of a real number.
c. Solve applied problems involving addition of real numbers.

Objective a
Adding real numbers without using a number line.

Addition on a Number Line
To do the addition a + b, we start at 0. Then we move to a, and then move according to b.
a) If b is positive, we move b to the right.
b) If b is negative, we move b to the left.
c) If b is 0, we stay at a.

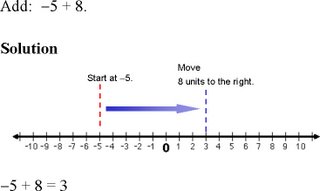
Example A



Example B



Rules for Addition of Real Numbers
1. Positive numbers: Add the same as arithmetic numbers. The answer is positive.
2. Negative numbers: Add absolute values. The answer is negative.
3. A positive and a negative number: Subtract the smaller absolute value from the larger. Then:
a) If the positive number has the greater absolute value, the answer is positive.
b) If the negative number has the greater absolute value, the answer is negative.
c) If the numbers have the same absolute value, the answer is 0.
4. One number is zero: The sum is the other number.

Example C



Example D



Example E



Objective b
Find the opposite, or additive inverse, of a real number.

Opposites, or Additive Inverses
Two numbers whose sum is 0 are called opposites, or additive inverses, of each other.

Example F



Symbolizing Opposites
The opposite, or additive inverse, of a number a can be named -a (read “the opposite of a,” or “the additive inverse of a”).

The Opposite of an Opposite
The opposite of the opposite of a number is the number itself. (The additive inverse of the additive inverse of a number is the number itself.) That is, for any number a
-(-a) = a.

Example G

Evaluate -x and -(-x) when x = 12.

Solution
We replace x in each case with 12.
a) If x = 12, then -x = -12 = -12

b) If x = 12, then -(-x) = -(-12) = 12

Example H

Evaluate -(-x) for x = -7.

Solution
We replace x with -7.

If x = -7, then -(-x) = -(-(-7)) = -7

The Sum of Opposites
For any real number a, the opposite, or additive inverse, of a, expressed as -a, is such that
a + (-a) = -a + a = 0.

Example I

Change the sign (Find the opposite.)
a) -9 b) 8

Solution
a) -9 -(-9) = 9

b) 8 -(8) = -8

Example J