Introduction to Real Numbers and Algebraic Expressions 1.7
1.7 PROPERTIES OF REAL NUMBERS
a. Find equivalent fraction expressions and simplify fraction expressions.
b. Use the commutative and associative laws to find equivalent expressions.
c. Use the distributive laws to multiply expressions like 8 and x – y.
d. Use the distributive law to factor expressions like 4x – 12 + 24y.
e. Collect like terms.
Objective a
Find equivalent fraction expressions and simplify fraction expressions.


Example A

Objective b
Use the commutative and associative laws to find equivalent expressions.
Example B
Evaluate x + y and y + x when x = 7 and y = 8.
Solution
We substitute 7 for x and 8 for y.
x + y = 7 + 8 = 15
y + x = 8 + 7 = 15
Example C
Evaluate xy and yx when x = 7 and y = 8.
Solution
We substitute 7 for x and 8 for y.
xy = 7(8) = 56
yx = 8(7) = 56

Example D
Calculate and compare:
4 + (9 + 6) and (4 + 9) + 6.
Solution
4 + (9 + 6) = 4 + 15
= 19
(4 + 9) + 6 = 13 + 6
= 19

Objective c
Use the distributive law to multiply expressions like 8 and x – y.

Example E

Example F


Objective d
Use the distributive laws to factor expressions like 4x – 12 + 24y.

Example G

Example H

Objective e
Collect like terms.
A term is a number, a variable, a product of numbers and/or variables, or a quotient of two numbers and/or variables.
Terms are separated by addition signs. If there are subtraction signs, we can find an equivalent expression that uses addition signs.
The process of collecting like terms is based on the distributive laws.
Like Terms

Example I
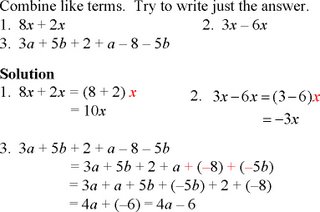

0 Comments:
Post a Comment
Subscribe to Post Comments [Atom]
<< Home